Building custom magnetic field coils, pulsed power systems, and scientific instrumentation since 2005
Equilibrium
Several tools are in use at WSI for exploring equilibria in magnetic fusion systems. Primarily we use CORSICA for most of the major systems under study, however sometimes it is easier to set up an initial condition for MHD simulations with NIMEQ. For the development of new magnetic configurations (say we are designing a tokamak from the ground up), then we use both FIESTA and CORSICA at the same time, in part to give a check of the configuration, and in part because FIESTA is so easy to use. We also got involved with other equilibrium solvers over time, so have a small library of Matlab and FORTAN based models (such as Leuers EQLFE) which come in handy occasionally when coding up something straightforward.
CORSICA
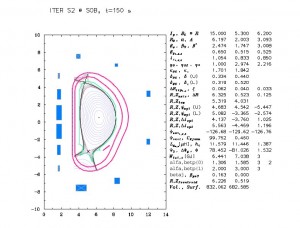
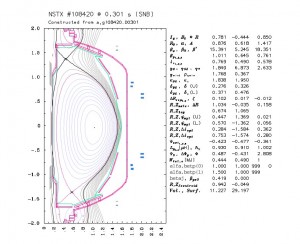
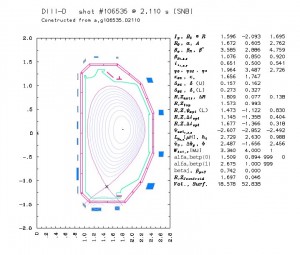
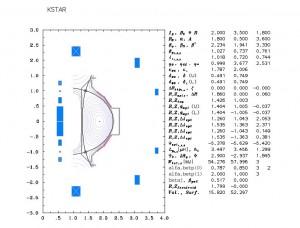
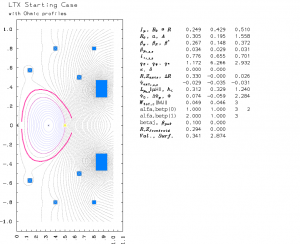
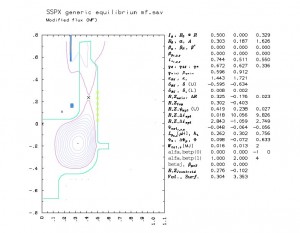
The LLNL CORSICA code provides a comprehensive predictive capability for axisymmetric toroidal plasmas. It has been applied successfully to many tokamaks, to the SSPX spheromak, and to the reversed-field pinches MST and RFX. At the heart of CORSICA is a 1.5-D, time-dependent plasma simulation code which solves the Grad-Hogan problem: self-consistent evolution of free-boundary plasma equilibria and internal profiles, including external conductors and magnetic diffusion, with a variety of available transport models.
CORSICA Wiki
CORSICA References
DCON
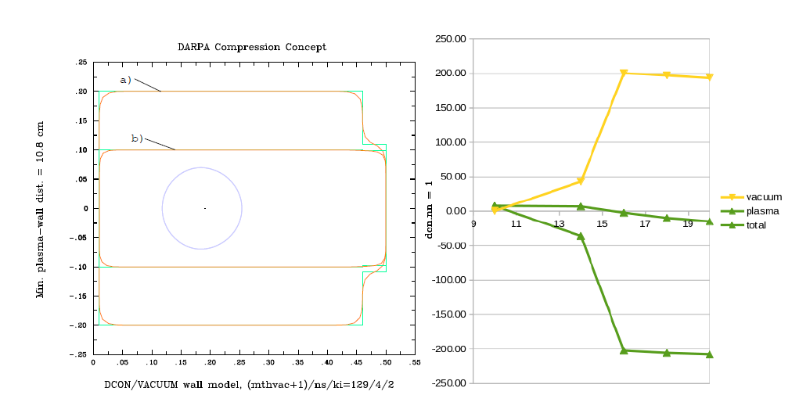
We examine the stability of plasmas with the DCON code (A. H. Glasser Physics of Plasmas 23, 072505 (2016) ). Shown are: left) Geometry variation for the tilt stability study and right) energies computed by DCON, showing a transition to stable at 14cm. DCON finds all modes stable for nn = 1 up to a stabilizing plate height of 14cm.
Fiesta
Fiesta started life as a simple forward equilibrium solver, but since then has been expanded into a toolbox for dealing with many equilibrium related problems. It can do the forward problem with a range of control methods, as well as the inverse (efit) problem, also with considerable flexibility. Once an equilibrium has been calculated, there are extensive facilities for calculating things like the q profile, global quantities (beta, li etc), signals from a range of sensors, field line following, and so on. Extra facilities now include the CRPP RZIp algorithm for control system design, a time domain model for the passive structure, and a full time domain plasma model is under development. It is also fairly simple to link up with the vector3/magint package to calculate error fields and such like.
NIMEQ
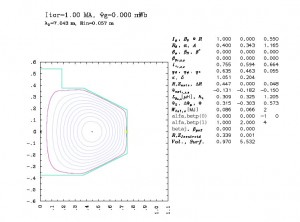
A Grad-Shafranov equilibrium solver is developed within the NIMROD framework to create plasma profiles for realistic geometry. The traditional Grad- Shafranov operator is converted to a pure divergence allowing the use of standard regularity conditions for the quantity Psi/R^2 in simply connected domains. The resulting equation is solved in the weak form using a finite element representation. A Picard scheme is used to advance the nonlinear iteration.
Download Eric Howell's APS Presentation on NIMEQ (pdf)
EQLFE
EQLFE is a set of Matlab scripts to solve the Grad-Shafranov equation for compact torus (CT, no hole through the middle) plasmas, written by Jim Leuer and Mike Schaffer at GA. The equations (essentially their signs) are written for a conventional right-handed cylindrical coordinate system (R, toroidal angle, Z). Units are SI (mksA). The magnetic separatrix is free and is found self-consistently by iteration. Pressure and poloidal current (B_toroidal) profiles can be specified with some degree of flexibility. FRCs, spheromaks, mixtures, doublets and other CT configurations can be made at present. The user can write and use custom profile routines.